Notion de Champ

On définit un champ, scalaire ou vectoriel, par considération d'une grandeur physique sur une photo de l’espace prise à l’instant t.

Par découpage de cet espace, la grandeur qui y est représentée au point M est considérée constante dans le volume dτ.

Prenons pour exemple un écoulement fluidique, i.e. un champ du vecteur vitesse des volumes dτ qui composent ce fluide, et intéressons-nous à une partie de fluide (une goutte d’huile par exemple) englobant le point M à la date t.

En considérant les vitesses de toutes les particules dτ qui composent cette partie à la date t, on peut prévoir la position et la forme de cette goutte d’huile à la date t+dt.

A cette date, le point M n’en fait peut être plus partie. Le point M est resté ancré à la photo, aux coordonnées qui étaient les siennes à la date t. C’est la différence entre la vision Laplacienne (pour laquelle on suit les particules) et cette vision Eulérienne.

Le flux d’une grandeur vectorielle à travers une surface est une notion très importante en Electromagnétisme.

Du point de vue de la définition, elle se cantonne à un produit scalaire :

Physiquement, si le vecteur dont on calcule le flux représente une densité volumique de débit, alors le flux calculé par la formule précédente sera égal au débit à travers la surface considérée (voir le paragraphe sur la densité volumique de courant par exemple)

C’est le sens du vecteur surface qui impose le sens dans lequel on considère le flux.

Le calcul d’un flux entrant dans une surface fermée se fait en considérant un vecteur surface dirigé vers l’intérieur du volume.

Le calcul d’un flux sortant d’une surface fermée se fait en considérant un vecteur surface dirigé vers l’extérieur du volume.

Une ligne de champ est une des représentations graphique possible pour un champ. Elle est définie telle qu’en chacun de ses points M elle est tangente au champ A qu’elle représente.

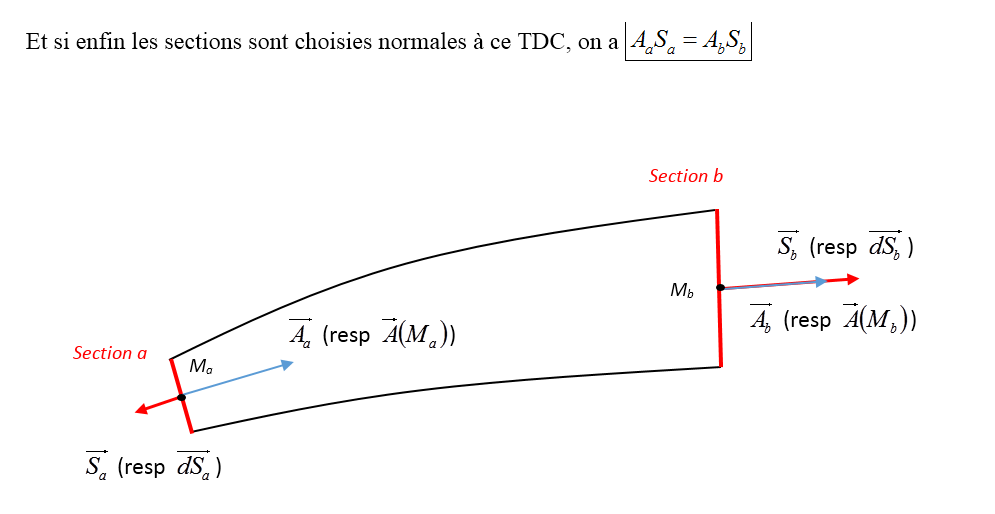
Un tube de champ est une région de l’espace délimité par des lignes de champ. Sa coupe dans un plan est délimitée par 2 lignes de champs

La propriété fondamentale d’un TDC est que le flux du champ associé sur la surface latérale est nul (puisque le champ y est partout tangent)

On considère souvent un TDC élémentaire, i.e. un TDC sur la section duquel le champ considéré est forcément homogène (section dS)

On dit qu’un champ est à flux conservatif lorsque, si l’on considère une surface fermée, « tout ce qui rentre est égal à tout ce qui sort »