Le magnétostatisme défini jusqu’ici s’applique uniquement
dans le vide (dans l’air … c’est presque pareil), en considérant des sources de
courant qui se baladent dedans.
Un « milieu » est une partie de l’espace susceptible de
modifier le champ B
Nous verrons que la modification qu’apporte ce milieu au
champ
peut être modélisée
par une considération de courant supplémentaire, dits d’aimantation (jaim) qui vient se superposer aux courants « réels »,
que l’on qualifie de libres pour éviter les confusions (j ou jl)
L’exemple ci-dessus sera à garder en tête : un milieu
ferromagnétique a tendance à conduire le flux magnétique. Alors que la bobine
dans le vide induit un champ qui se disperse « librement » dans
l’air, la bobine enroulée autour d’un circuit fermé ferromagnétique induit dans
ce dernier un champ homogène (les LDC restent parallèles entre elles), et qui
ne fuit pas hors du matériau.
Notons :
·
Que le circuit magnétique « a
tendance » à conduire le flux, mais ne le conduit pas
obligatoirement : si on fabrique un circuit fermé de 3km de long et qu’on l’entoure
de 3cm de bobine, on sent bien que les LDC vont se reboucler dans l’air plutôt
que de parcourir ces 3km
·
Que, comme pour tout champ homogène, le
rotationnel de B est nul : en aucun point du circuit magnétique on note un
effet « tourbillon », c'est-à-dire un point atour duquel l’induction
a tendance à tourner sur elle même
Le champ magnétique H et le champ d'aimantation M:
L’induction B en ce point est la superposition de
cette excitation et de la réaction, appelée champ d’aimantation et notée M (on
parle aussi de J=M/µ0)
Notons bien que H n’est pas l’induction B qui
serait présente en l’absence totale du matériau : au point M où autour
duquel on évide le matériau, l’induction (dans le vide donc) dépend (outre des
sources) de la réaction du matériau en tous les autres points du matériau.
Cette réaction aux autres points dépend elle-même de l’excitation en ces points
…. On retrouve là encore toute la complexité de la superposition des phénomènes
physiques.
La réaction du matériau en un point N est du type :
« il y a une excitation, le matériau la booste en y superposant une
induction additionnelle M »
Dire que cette réaction « provoque » un champ de
réaction Hréaction au point M est une notion assez floue. Ce n’est
pas un champ qui est source d’un autre champ, mais des charges électriques en
mouvement.
On modélise généralement M comme résultante de
l’apparition de courants d’aimantation. Et ce sont ces courants qui induisent
le champ de réaction. Cette modélisation intuitive reflète l’alignement
physique des spins d’électrons au sein d’un matériau ferromagnétique soumis à
une induction externe.
Au final, la modélisation du comportement des matériaux
ferromagnétiques passe par
·
Une méthode pragmatique, qui consiste à relever
par expérience la réaction d’un matériau soumis à une excitation connue. Mais
cela ne suffit pas, car il reste toujours à connaître l’excitation au point M
avant de se référer au résultat de cette expérience pour connaître la valeur de
la seule grandeur qui nous intéresse, l’induction B.
·
La modélisation de la réaction du matériau par
l’intégration des courants d’aimantation dans les équations de Maxwell. En
effet, celle-ci nous permettra la détermination du champ H en tout point de
l’espace (et par conséquent, pour un matériau connu, la connaissance de B)
La courbe B-H:
La courbe B-H:
La première caractérisation d’un matériau est pragmatique :
il s’agit, pour plein de valeurs d’excitations H possibles, de mesurer la résultante
B. Notons que B est la seule grandeur mesurable : c’est bien l’induction,
et non autre chose, qui est source d’une force (sur les électrons)
Par retranchement de H à B, nous pouvons faire toujours
apparaître J, mais le tracé de la courbe B-H est plus usuel que celui de la
courbe J-H.
Attention : savoir à quelle excitation H on travaille
n’est pas trivial. Il est hors de question de faire un petit trou dans le
matériau à caractériser pour aller y mesurer B et le diviser par µ0
(quoique, au moins, cette méthode serait réfléchie)
·
Soit on injecte un stimulus quelque part dans un
montage d’essai, dont sait par calcul qu’il va produire l’excitation souhaitée
(y’a pas intérêt à se tromper dans les calculs)
·
Soit on mesure B à un endroit du montage
d’essai, en sachant que cet endroit se comporte comme une partie évidée du
matériau à analyser
Nous reviendrons plus tard sur les méthodes de
caractérisation de la courbe B-H.
Intéressons-nous au résultat.
On peut dissocie 2 types de courbes B-H :
·
Les courbes simples, qui vues de loin font
apparaître une proportionnalité entre B et H tant que le matériau n’est pas
saturé : on parle de matériaux ferromagnétiques doux.
·
Les courbes à hystérésis : celles qui font
apparaitre une relation différentes entre B et H selon l’historique du matériau
(la manière dont il a été excité avant) On parle de matériaux ferromagnétiques
forts. Les aimants font partie de cette famille.
Nous avons donc 2 notions à détaillées (en plus de la
réaction la plus simple d’un matériau ferromagnétique) : la saturation
d’un matériau (à laquelle est soumise tout matériau, doux ou fort) et
l’hystérésis.
Perméabilité relative :
Quand un volume élémentaire de matériau est soumis à une excitation
externe (H(N) sur le schéma précédent), une force agit sur ces électrons qui
ont tendance à aligner leurs trajectoires, induisant ainsi un champ propre
(M(N)) qui booste l’excitation source. La plupart du temps ce coup de booste se
fait dans la même direction que le l’excitation. Par contre, il n’est pas rare
que ce coup de boost marche moins bien dans certaines directions (on parle de
matériau anisotrope)
Toujours est-il que ce coup de boost se traduit par une
réaction proportionnelle à l’excitation :
De cette relation de proportionnalité découle directement
une relation de proportionnalité entre B et H :
Les termes µ0 et 1+ χ ne sont pas regroupés
directement sous un seul et même coefficient de proportionnalité : 1+ χ,
terme sans dimension, décrit justement le coup de boost que le matériau apporte
à l’excitation par rapport à la relation entre B et H dans l’air. Ce terme est
appelé perméabilité relative, et est noté µr :
·
Dans le vide, µr=1
·
Dans un matériau ferromagnétique µr
atteint généralement plusieurs centaines
Pour la simplicité de l’écriture, le produit µ0µr
est regroupé sous le µ, que l’on appelle « perméabilité du matériau »
Si l’on regarde le matériau de loin, on peut souvent considérer
la perméabilité du matériau comme une constante, qui ne dépend pas de H.
Si l’on regarde le matériau de plus près, alors on s’aperçoit que cette
grandeur dépend de l’excitation, surtout dans les H faible. Il faut alors
considérer la perméabilité locale :
Saturation d’un matériau :
Un matériau sature lorsque, malgré l’augmentation de
l’excitation qu’il subit, il n’y a plus d’augmentation de sa réaction : B
augmente avec H de la même manière qu’il le fait ans l’air.
Dans la partie saturée, on a donc
Hystérésis :
Première remarque, une bonne fois pour toutes : le
mote Hystérésis est féminin. On ne dit pas « un hystérésis » mais
« une hystérésis », ou « une hystérèse » Ces 2 synonymes
ont pour définition :
Propriété d’un système ou d’un matériau dont l’état dépend de l’histoire des sollicitations auxquelles il a été soumis, ou du
sens de variation de ces sollicitations.
L’hystérèse existe dans la plupart des matériaux
ferromagnétiques, mais dans le dimensionnement des systèmes magnétiques, on ne
le prend souvent en compte que pour les aimants : un aimant est un
matériau ferromagnétique qui est utilisé justement pour ses caractéristiques de
rémanence.
Prenons donc cet exemple particulier qu’est
l’aimant : il est particulier en cela qu’en dehors de sa courbe de désaimantation,
sa perméabilité est proche de celle de l’air. En effet, la perméabilité d’un
aimant, en dehors de sa courbe de désaimantation, est proche de celle de l’air.
En gros, un aimant, c’est de l’air avec une rémanence.
La caractéristique B-H d’un aimant « non
aimanté » suit une courbe dite de première aimantation.
Si on amène son excitation H jusqu’à saturation (C),
alors la redescente
de H provoque une diminution de B sur une pente externe du cycle d’hystérésis.
Comme précisé plus haut, la pente de cette caractéristique est proche de celle
de l’air (µ0) Si l’on diminue H jusqu’à l’annuler (D), alors
l’induction correspondante est égale à ce que l’on appelle l’induction
rémanente, et est notée Br : c’est l’induction résiduelle présente dans le
matériau sous une excitation nulle. Notons bien qu’un aimant sous excitation
nulle n’est pas l’état d’un aimant seul dans le vide : la présence d’une
rémanence dans le voisinage du point M appartenant au matériau est source d’une
excitation au point M, dans le sens opposé à la rémanence (le volume dτ auquel
on s’intéresse a plus de voisins qui lui impose un champ externe négatif que de
voisins qui lui imposent un champ externe positif) Un aimant seul dans le vide a donc un point de
fonctionnement à H<0 (E)
Continuons à
diminuer H, mais en restant sur cette partie linéaire (F) : à tout moment,
si l’on décide de le ré augmenter, on va ré augmenter B en suivant cette droite
… jusque là c’est logique.
Rediminuons H
et entamons la rupture de pente qui marque la courbe de désaimantation (jusqu’au
point G) : Toute remontée de l’excitation se fera avec la pente, non pas
de la courbe de désaimantation, mais la pente de la partie linéaire : le
chemin suivi s’appelle la droite de recul. Si l’on revient à excitation nulle
par exemple, on ne va revenir à la rémanence atteinte initialement, mais à une
autre, plus faible (K)
Si on avait diminué H jusqu’à la
saturation, alors une ré augmentation nous fera suivre le chemin externe
inférieur du cycle d’hystérésis. A champ nul, l’induction est égale à sa valeur
de rémanence, mais dans le sens opposé.
Nous voyons donc qu’une infinité chemins existe au sein
même d’un seul et même cycle d’hystérésis maximal.
Et encore, cela n’est qu’une approximation qui arrange
bien nos dimensionnements, car si l’on regarde de près :
·
La pente de la droite de recul n’est en fait pas
égal à la pente de la partie linéaire externe (ici approximée à µ0) :
cette droite est légèrement plus pentue que la pente externe, ce qui fait que
si l’on n’est pas partis trop loin dans la désaimantation, on a des chances de
rejoindre le cycle externe.
·
La droite de recul n’est en fait pas une droite,
mais elle-même un cycle d’hystérésis interne
Reprenons la définition de H :
Nous avons, en ce point « surfacique »:
En effet, M étant nul sur la face supérieure du matériau, car appartenant par convention à l’extérieur,
Soit,
D’autre part:
Equations de magnétostatisme dans les milieux:
TAAADDDAAAAA ... on en est venu à bout: on peut enfin exprimer les équations de magnétostatisme dans les milieux, et sans omettre comme cela est souvent le cas dans la littérature, l'expression des courant d'aimantation surfaciques:
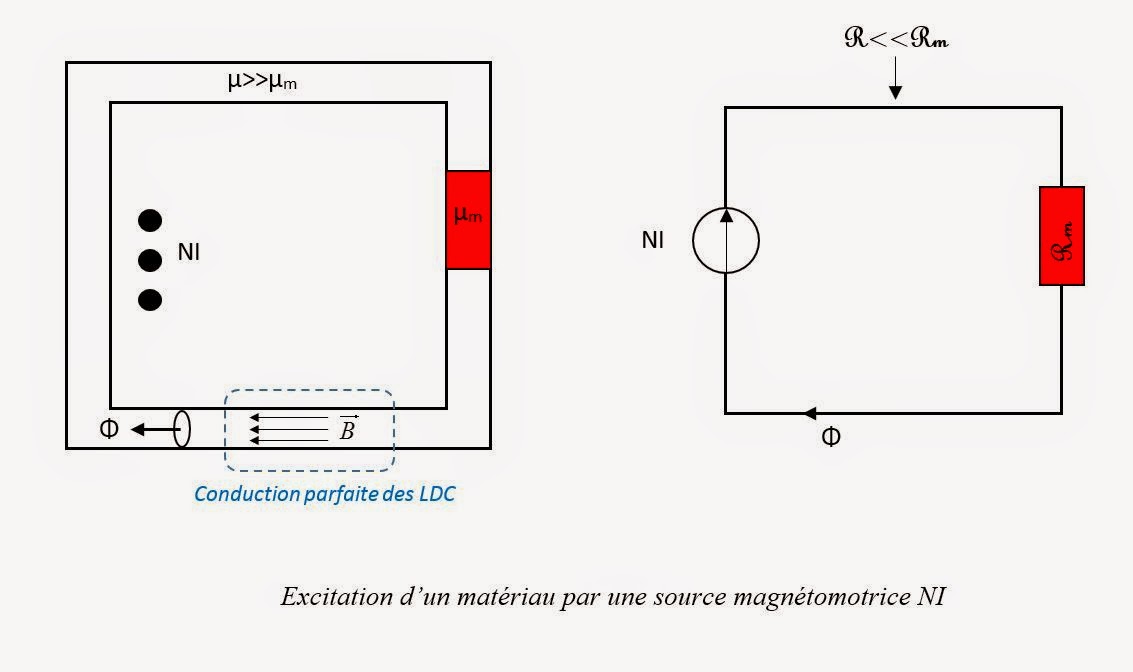
L'analogie électrique:
On a
Soit, de manière générale :
Le terme:
En effet, de ce que l’on a vu des matériaux rémanents, si l’on excite un
matériau ferromagnétique via un aimant via une jonction de reluctance nulle, on
a :
D'autre part:
Alors nous pouvons écrire que:
Puisque M est placé dans le vide, alors on peut y
appliquer les équations du magnétostatisme dans le vide, on a alors :
où jl est la densité de courant dans ce volume
dτ « rempli de vide » Cette densité de courant exclut donc tout
courant d’aimantation : il ne s’agit que de sources « libres »
(d’où la notation jl)
D’autre part, si l’on considère le point M, dont le volume élémentaire
dτ qui l’entoure peut être considéré comme un volume « rempli de vide dans
lequel circule des courant d’aimantation », on peut exprimer directement
le rotationnel de B :
Et puisque
alors l’expression précédente revient à:
Enfin, si l’on réinjecte la propriété (1) dans
cette expression, il vient finalement :
Nullité de jaim dans un milieu linéaire:
Supposons un matériau ferromagnétique linéaire,
dans lequel, par définition
Puisque
alors il vient
On rappelle que χ, facteur de linéarité entre l’excitation
H et la réaction locale M est appelé susceptibilité magnétique.
Supposons que ce matériau ferromagnétique ne soit
pas parcouru par des sources libres (ce qui est généralement le cas), alors:
D’après la relation entre M et H que nous venons
d’établir pour un matériau linéaire, alors cela équivaut à:
Et puisque:
alors cela signifie que
·
Pour un matériau ferromagnétique linéaire
·
Non parcouru par des sources libres
Alors le vecteur d’aimantation volumique est nul :
Le résultat de cette démonstration très mathématique pouvait être prévu en réfléchissant un peu.
Supposons un milieu (ou un morceau de milieu) dans
lequel H est unidirectionnel. Son irrotationnalité, imposée par l’absence de
sources libres, équivaut alors à une homogénéité (si H n’était pas homogène
alors son rotationnel ne serait pas nul)
Si H est homogène dans le matériau, c’est que la réaction
de ce matériau l’est aussi. Cette réaction peut être vue comme l’apparition de
spires de courants autour de chaque volume élémentaire dτ.
En fait, les courants d’aimantation volumiques correspondent à la
densité volumique de ces spires (non démontré ici), ou plus exactement à la densité volumique des
moments magnétiques :
Dans un milieu homogène, on se retrouve donc avec
une juxtaposition de spires de courants d’aimantation dont chaque branche
s’annule avec la branche voisine. Au final, la superposition de ces spires est
nulle. On retrouve donc le fait que la circulation totale des courants
d’aimantation est nulle.
Les courants d'aimantations surfaciques:
Mais ce résultat est valable tant qu’il y a des spires
voisines. En surface du matériau subsiste un courant surfacique non nul. Là
aussi ce résultat pouvait être prévu. Supposons notre exemple de matériau
conducteur autour duquel est bobiné un fil :
·
L’excitation est provoquée par le bobinage
autour du matériau
·
La réaction, si elle est proportionnelle à cette
excitation, doit avoir la même forme, i.e. un « bobinage » autour du
matériau.
Ce bobinage de réaction appartient au matériau, et dans le même temps
est disposé autour de ce dernier : il ne prend donc de valeur qu’à
l’interface entre les 2 milieux, i.e. à la surface du matériau.
Donc au final on aura bien plus souvent de courants
surfaciques sur un matériau ferromagnétique que de courants volumiques.
Il faut donc les quantifier. Nous utilisons pour cela la
correspondance densité volumique/densité surfacique
On considère un point M(x,y,z) situé sur la dernière
tranche (selon un découpage volumique) d’un matériau ferromagnétique:
Nous avons, en ce point « surfacique »:
D’une part:
En effet, M étant nul sur la face supérieure du matériau, car appartenant par convention à l’extérieur,

Soit,
D’autre part:
Finalement on a, quelque soit l’orientation du
repère (x,y,z) choisi:
Cela entraîne que, en tout point appartenant à la
surface d’un matériau ferromagnétique (quelque soit sa nature), on a
avec:
·
js le courant
d’aimantation surfacique
·
M le vecteur aimantation
en un point de la « surface » (dernière tranche du découpage
volumique du matériau)
·
n le vecteur unitaire
normal à la surface du matériau
TAAADDDAAAAA ... on en est venu à bout: on peut enfin exprimer les équations de magnétostatisme dans les milieux, et sans omettre comme cela est souvent le cas dans la littérature, l'expression des courant d'aimantation surfaciques:
Où :
·
H est le champ magnétique, i.e., à une constante
µ0 près, l’induction magnétique au point considéré si le volume
élémentaire dτ autour de ce point était rempli de vide.
·
jl est la densité volumique de
courant libre
·
jaim est la densité volumique de
courant d’aimantation. Cette grandeur est nulle dans un matériau linéaire dans
lequel il n’y a pas de sources libres
·
js est la densité surfacique de
courant d’aimantation. Cette grandeur représente souvent l’essentiel de la
réaction M d’un matériau à l’apparition d’une excitation H
·
n est le vecteur normal unitaire de la surface
du matériau (dirigé vers l’extérieur du matériau)
Et voilà le passage le plus important de cette partie sur
l’électro magnétisme…
Partons de la propriété de conservation du flux de l’induction. On peut
assimiler le flux de B
Pour que cette analogie serve à quelque chose, il
va falloir trouver une grandeur X à identifier à U et une grandeur Y à
identifier à R telles que X=Y.Φ
Puisque nous avons déjà exploité la propriété
, il ne nous plus reste pour cela que
Mais l’analogie électrique traite de grandeurs
globales … nous considérons donc la forme globale du théorème d’Ampère, soit
(Ienlacé étant le courant total enlacé
par le chemin fermé L=NI si ce courant est discrétisé par le passage de N fil
dans lesquels débite le même courant I)
Nous considérons comme chemin fermé L le chemin que
suit un TDC, que ce chemin passe ou non par différents
matériaux, pourvu que ces matériaux soient linéaires
On a
Découpons le chemin L en tronçons, selon que L soit
dans un matériau ferromagnétique ou dans l’air :
Soit, de manière générale :
avec Lk le tronçon de (L) dans le
matériau k
Or, en tout point du chemin :
Pour chaque tronçon du TDC considéré, on a
donc :
Aussi, puisque l’on se place dans un TDC, B est
colinéaire à tout déplacement élémentaire dl sur le chemin (L) :
où dS est la section normale du TDC
On a donc, pour chaque tronçon du TDC
considéré :
Et puisque le flux Φ est conservatif (c’est le même
pour toute position considérée sur L), alors
Au final, le long d’un TDC refermé sur lui-même, et
traversant différents matériaux k on
a
avec
où:
- µk est la perméabilité est la perméabilité du matériau k
- dS est la section normale au TDC (orthogonale au déplacement dl dans ce TDC)
Le terme:
est appelé reluctance du matériau, et est noté R.
Cette expression se rapproche de l’expression d’une
résistance électrique:
où σ est la conductivité du matériau de longueur L,
aux bornes de laquelle une différence de potentiel U va donner naissance à un
courant I tel que I=U/R. Cette différence de potentiel U est appelé force
électromotrice. On montre qu’elle est égale à la circulation du champ E le long
du conducteur ohmique
Par analogie on nomme donc la circulation de H force
magnétomotrice.
Ici, on peut voir le tronçon k de reluctance Rk comme pouvant être excité par une différence de
potentiel
Tout comme une résistance électrique doit être
excitée par une source de tension U pour générer un courant I=U/R, ce tronçon
doit être excité par une source magnétomotrice (source de circulation de H)
pour se voir traverser par un flux Φ=HL/R.
- dans le cas de la résistance, on raccorde R au générateur par 2 fils de résistance nulle
- dans le cas du tronçon de matériau, il faudrait le raccorder au générateur par des tronçons de reluctance très faible par rapport au tronçon étudié
La source magnétomotrice la plus courante est le passage
de boucles de courant à l’intérieur du circuit de reluctance que l’on
considère.
Mais attention : le passage d’ampères-tours n’est pas
le seul moyen d’imposer une force magnétomotrice : on peut aussi utiliser
un aimant.
On note au passage que Ha, le champ dans
l’aimant, est opposé au flux dans le circuit.
On a donc:
Or:
et on note
avec Φr le flux dans l’aimant si son
induction était égale à son induction rémanente (si champ était nul donc)
Finalement:
En électricité, cette équation est caractéristique
d’une source de courant Φr imparfaite (résistance parallèle Ra):






























































Aucun commentaire:
Enregistrer un commentaire